《The Pudding》的編輯羅素‧哥登堡（Russell Goldenberg）和工程師安柏‧湯瑪斯（Amber Thomas）製作了一個小遊戲實驗，鍵盤上只能按出G和降E和弦的音，接著讓電腦隨機按鍵盤，觀察需要嘗試多少次才能彈奏出正確的旋律？在經過12次嘗試後，電腦成功彈奏貝多芬的《第5號交響曲》前奏。但為什麼要進行這個實驗呢？因為他們想讓讀者相信「無限猴子定理」。

　　根據維基百科的說明：「無限猴子定理的表述如下：讓一隻猴子在打字機上隨機地按鍵，當按鍵時間達到無窮時，幾乎必然能夠打出任何給定的文字，比如莎士比亞的全套著作。這個理論說明把一個很大但有限的數看成無限的推論是錯誤的。猴子精確地通過鍵盤敲打出一部完整的作品比如說莎士比亞的《哈姆雷特》，在宇宙的生命周期中發生的機率極其低，但並不是零。」

　　在回到音樂話題前，究竟猴子敲打出莎士比亞的作品可能性有多少？即使不加標點符號讓猴子打出《哈姆雷特》，這個可能性也小到難以想像。

　　假設每個鍵盤有26個英文字母，那就是（1／26）x（1／26）x（1／26）……一直乘下去約130,000次，才大約等於《哈姆雷特》的文本長度。為了理解這個瘋狂的機率從何而來，話題再回到貝多芬，我們該如何計算只得到前面兩個正確音符的機率呢？

　　隨著彈奏更多音符，成功機率會變得越來越渺茫。可能性將隨著每個新的音符出線而呈指數增長，但機率永遠不會是零。莎士比亞的作品或許似乎「永遠」也打不出來，但假如我們真的能夠永生，那這件事（幾乎肯定）可以實現。

　　雖然貝多芬旋律出現的可能性不斷遞減，但它還是有可能很快就會出現。羅素和安柏的實驗稍微作了弊，他們設定所有音符都是相同的音長。如果把每個音符再加上兩種可能的音長時，機率會發生什麼變化？

　　結果表明，總共試了126次才成功。

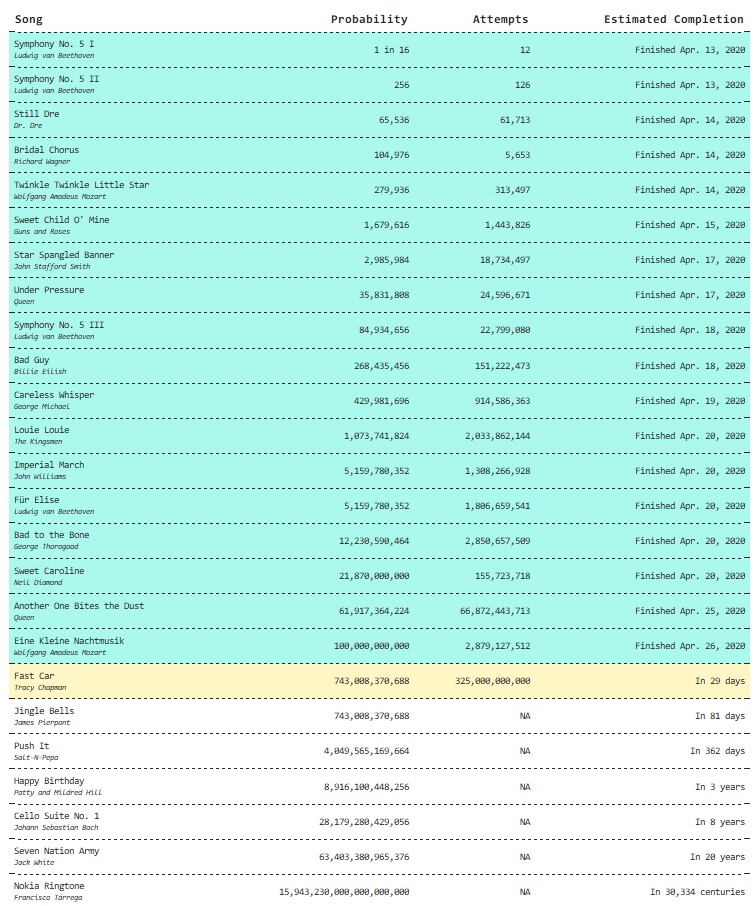
　　羅素和安柏精心設計出一個真實的實驗，從2020年4月14日開始執行。他們要求電腦每分鐘執行數百萬次的隨機嘗試，來加速實驗結果。每當電腦有所突破時，他們會透過增加旋律長度、音長時間或鍵盤數量逐步添加複雜性。

　　說了這麼多，做了這麼多，羅素和安伯的重點並不是單純呈現數字，而是希望讓人們明白只要有足夠的時間，隨機是有可能成真。這個實驗在我們的有生之年能彈出簡單的諾基亞手機鈴聲嗎？幾乎可以肯定不會。但如果有足夠的時間呢？幾乎可以肯定總有一天會發生。

原文出處：Pudding