編譯｜Mumu Dylan

　　退休的德國業餘統計學家托馬斯‧羅恩（Thomas Royen）在2014年7月17日早晨起床刷牙時，靈光一閃解開了困擾專家學者超過半世紀的數學難題：連結幾何、機率和統計學的著名猜想：「高斯相關性不等式」（Gaussian correlation inequality）。

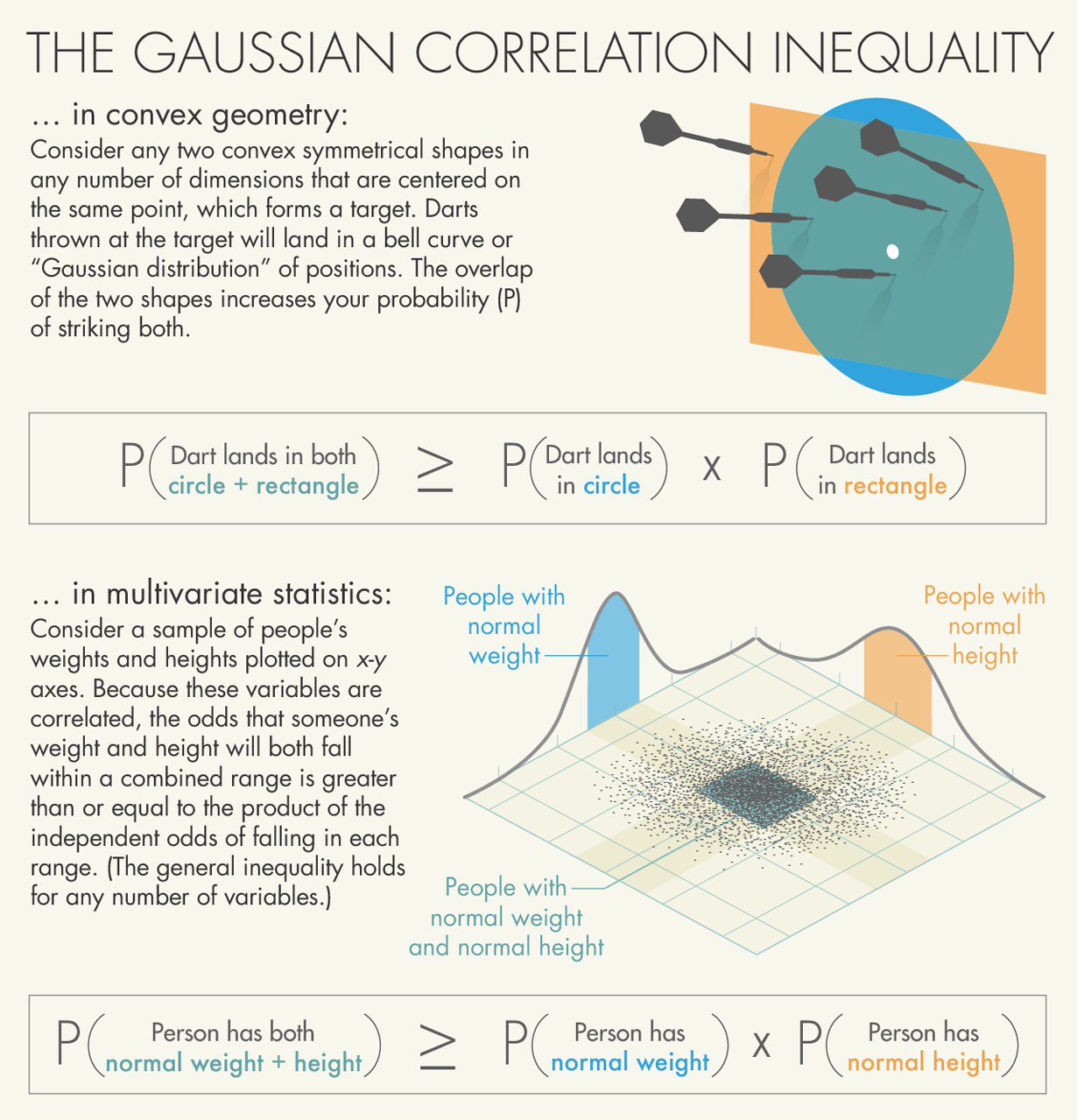
　　試想兩個如矩形和圓形的凸多邊形，相互重疊有著相同的中心點，接著以正中紅心為目標扔擲飛鏢，落點會呈現鐘形的高斯分佈（或稱常態分佈）。而高斯相關性不等式猜想，飛鏢落在圓形和矩形的交集機率，會大於或等於落在圓形的機率乘以落在方形的機率。簡單來說，由於兩個形狀重疊，因此射中其中一個形狀也會增加另一個形狀被射中的機率。猜想還認為任何兩個具有相同中心點的凸多邊形，在任何維度的情況下都能成立。

　　這則看似簡單的問題最初是由美國統計學家奧利弗‧鄧恩（Olive Dunn）在1959年提出，並在1972年衍伸為最著名的「射飛鏢」版本，自此之後便成為數學界公認的難題。賓州大學統計學家唐納‧理查茲（Donald Richards）表示：「我知道有些人花了四十年時間想證明出來，而我自己則已經嘗試了三十年。」

　　高斯相關性不等式的特殊型態，已經在1977年由維吉尼亞大學洛倫‧皮特（Loren Pitt）證明出猜想在二維情況下能成立。但是要證明試用於所有形態，仍然讓所有數學家頭疼。皮特自1973年以來就不斷地在嘗試證明，他回憶最初在一場會議從同事言談間得知這則猜想的故事：「作為一個年輕氣盛的數學家，我想說那些令人敬佩的數學家和科學家怎麼可能會不知道答案。於是我把自己鎖在旅館房間裡，非常相信自己走出房門後就能證明或反駁猜想。」然而，事情已經過了五十多年，皮特仍沒有找到答案。

　　羅恩在洗手台前想出證明以前，對高斯相關性不等式猜想並沒有太多想法。過去他是一間製藥公司的僱員，並在1985年進入德國賓根的一間小型科技大學，繼續鑽研許多產業統計人員所使用的藥物實驗數據公式。2014年7月羅恩已經退休，但仍致力於改進以前的公式，而他忽然想到高斯相關性不等式的統計分佈，或許能延伸運用至他長年研究的項目上，接著在17日早晨找到了證明猜想的方法，他說道：「當天晚上，證明的初稿就已經寫好了。」

　　然而，羅恩並不會使用數學界常用的論文編輯軟體「LaTeX」，只好在Word裡打下他所寫的計算公式。在隨後的一個月，他將論文發表在學術論文預印本網站「arXiv」上，並將它寄給了理查茲。「我透過羅恩的電子郵件看到這篇文章，當我看見它時立刻知道猜想已經被證明了。」理查茲說。

　　理查茲馬上通知幾位研究同事，協助羅恩使用LaTeX重新編寫論文，讓論文看起來更專業一點。但理查茲和羅恩所接觸到的其他專家學者，似乎沒有把他的巨大發現當作一回事。這是因為在過去幾十年一再地有人自稱解開了猜想，太多錯誤的證明使數學界感到厭倦，例如從2010年以來在「arXiv」網站上就曾出現過兩次。

　　臺拉維夫大學數學家伯阿茲‧克拉泰格（Bo'az Klartag）則回憶，光是在2015年就收到三封自稱解開猜想的電子郵件，其中包括了羅恩的證明。然而，當克拉泰格檢驗其中一封信件並發現錯誤時，時間不足的情況下他便把其他證明也擱置在旁，而羅恩的成果就這樣被忽略了。

　　一般來說，像羅恩這種重要發表通常會投稿至《統計年鑑》（Annals of Statistics）出版，然後全世界的學者都會看見。但是，羅恩考量後沒有投稿到頂尖期刊上，由於自己沒有足夠的研究資歷，加上頂尖期刊的審核流程往往很緩慢且要求很高，於是他最後選擇投稿至一間位於印度安拉阿巴德的《遠東理論統計期刊》（Far East Journal of Theoretical Statistics）上迅速地發表，但因為該期刊的發表者大多是名不見經傳的學者，因此根本沒有人注意到羅恩的證明。

　　最終在2015年12月，羅恩找到波蘭數學家拉斐爾‧拉塔拉（Rafał Latała）及其學生達里烏斯‧馬特拉克（Dariusz Matlak）幫忙，於「arXiv」網站上重新發表一篇含有羅恩證明的論文作為宣傳，他的成果才逐漸在全世界流傳。沒有人知道為何在21世紀，這麼重要的數學證明仍然傳播得如此緩慢。克拉泰格說：「很明顯這是在一個容易交流的時代缺少了交流，但無論如何我們最後還是看見了，而且他解得非常漂亮。」

　　羅恩希望自己的經驗能激勵所有的年輕學子運用創造力找出新的數學定理，因為這些事物並不總是需要很高深的理論水準。而他對自己的成果被忽視也沒有感到特別失望或訝異，他在一封電子郵件中寫道：「我早已習慣過去被德國頂尖大學的科學家多次忽視，我也不是那種非常有才華或人脈的研究者，我的生活也不需要功名來增添色彩。」對羅恩來說，解開重要的數學猜想的喜悅和滿足已經足夠，他說：「這就像是一種恩典，我們在一個問題上花了很長的時間努力，而突然一個天使詩意地觸動了我們神秘的神經元帶來了解決方法。」

參考報導：Quanta